T-PROGS
关于T-PROGS的简单介绍
T-PROGS是一个可以模拟地质岩性在三维空间中的随机分布的成熟软件,它原本是基于Fortran语言的开源软件包,现在的地下水模拟软件GMS软件系统中已经包含了该模块,可以直接在GMS中直接使用。本文的目的在于记录该软件模块的使用学习和过程记录。
为什么要使用T-PROGS
在地下水数值模拟的过程中,由于地下水系统属于巨复杂系统,将其复杂的运移过程简单的用一个微分方程的计算结果代替必然会产生大量的不确定性;另外模拟所需要的参数在获取过程中同样会带来各种各样的不确定性。目前的地下水数值模拟逐渐将目光集中到地下水模拟的不确定性分析上,在各种非确定分析方法中使用广泛的随机模拟方法最为常见。
随机模拟方法
地下水随机模拟主要有矩方程法和Monte Carlo法。矩方程法通过求解随机微分方程直接求取模拟结果的各阶统计矩;Monte-Carlo方法则是通过随机场生成器实现大量的确定模型,对这些实现的模拟结果进行统计分析得到模拟的统计特征。
在Monte-Carlo方法过程中涉及到随机参数场的生成。对渗透性这一参数而言,为了分析其在模拟过程中的不确定性大小,对其进行参数随机模拟,于是需要生成大量的渗透系数随机场。一般来说,渗透系数的自然分布满足对数正态分布的关系,在已知水文地质参数信息的帮助下通过各种条件模拟方法便可以模拟出未知点处的渗透系数概率分布情况,并基于此概率生成大量的确定参数场进行地下水数值模拟。
建模过程
此处涉及到水文地质概念模型建模过程的问题:1. 直接建模,在建立水文地质概念模型时直接输入所需要的各种边界条件,源汇项以及水文地质参数;2. 间接建模,在水文地质参数的建立过程中,并不是直接划分参数分区并给定相应的参数,而是先通过三维地质建模建立研究区的三维地质模型,再根据地质介质与水文地质参数之间的相互联系间接地建立水文地质参数场。间接建模的好处是考虑了自然情况下的物理因素(一般来说,误差范围内的水文地质参数就是由地质结构以及地层介质来决定的),减少了由于人为的参数分区而带来不确定性。
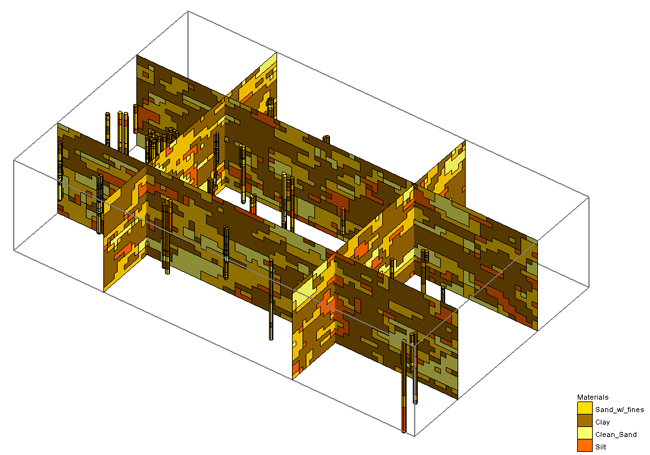
在此基础上,我们可以说实际上T-PROGS是一种基于马尔科夫链的“转移概率地统计(_Transition Probability Geostatistical_)”模型,用于生成地层岩性的三维随机分布。他主要处理的是类似钻孔信息的分类地质参数(指示地统计方法)。通过间接建模的方法利用T-PROGS便可以直接由钻孔数据得到渗透系数等水文地质参数的随机分布场,相对于其他方法更加占据优势,在国内外也得到了大量的应用。举例就不要举例了,又不是写论文……
理论与方法
地统计方法简单介绍
地质统计学的核心以及基础是”变差(变异)函数”:
空间中一点$x$与其相邻一点$x+h$的某一相关变量$Z(x)$方差的差值,称为$Z(x)$在$x$方向上的变异函数,记为$\gamma(x,h)$:
上式是在以为情况下成立的,高维情况都是以一维情况为基础,在二阶平稳场(简单来说就是$\gamma(x,h)$只与$h$有关,任何一点相同距离内的变差函数的均值都是一样的)中有:
如此一来,变异函数就被简化为一个单变量函数,并且在$x$方向上任取两点$x_i,x_i+h$对应的变异函数都是以$h$为自变量的随即变量的一个统计样本,其所有取值构成了一次统计。
对于克里金方法(Kriging Method)来说,空间中一点处某一参数$z$的估计值为:
其中$\hat{z_o}$是点处的估计值,即$z_o=z(x_o,y_o)$,$λ_i$是权重系数。克里金方法是用空间上所有已知点的数据加权求和来估计未知点的值。此处的权重是能够满足点 $(x_o,y_o)$处的估计值$\hat{z_o}$与真实值$z_o$的差最小的一套最优系数,即
同时满足无偏估计的条件:
求解简化(拉格朗日乘数法)之后可以得到下面的一组控制方程:
在上式中唯一未知的便是我们先前所提到的变差函数(或称变异函数,半方差函数;此处的$\overline\gamma(x_o,V)$表示以$(x_o,y_o)$为中心的一个空间范围$V$内所有的变差函数的均值)。事实上,根据地理学第一定律:距离越近空间相关性越强,我们可以简单地做出假设:
两点的变差函数与其距离之间存在某种函数关系,这种函数关系可以是线性、二次函数、指数、对数关系。
通过对数据集进行分析,从而寻找到一个最优的拟合曲线拟合距离$d$与变差函数$\gamma$的关系,得到函数关系式$\gamma = \gamma(d)$那么对于任意两点$(x_i,y_i)$,$(x_j,y_j)$,先计算他们之间的距离$d_{ij}$然后根据得到的函数关系就可以得到这两点的变差函数,进一步的解决空间中一点的参数估计问题。
马尔科夫链与转移概率地统计
转移概率是马尔科夫链的一个重要概念,马尔科夫过程假设事物后一时刻的状态至于前一时刻的状态相关。换句话说:今天的事情由昨天完全决定,明天的事情由今天完全决定,并且与此前的每一天都没有直接关系。在此基础上所谓转移概率就是从一种状态转变为另一种状态的概率,在地统计学中有如下的表达:
它表示已知$x$处的岩性为$j$,$(x+h)$处岩性为$k$的概率。
利用指示地统计中指示变量的形式($I_j(x)$)我们可以将变差函数转为下面的形式(协变差函数):
同时,将转移概率用指示变量表示:
PS:这里使用均值是一个统计过程,实际过程过我们不可能知道概率的实际大小,所以利用统计得到的两个事件各自在多个统计点发生的平均数之比来代替概率之比。事实上,在指示地统计中均值和概率是等价的。
紧接着,我们可以将转移概率和所谓协变差函数结合起来,找出它们的关系式:
作如下的假设:
特别的,我们有:$P_{jk}(0) = P_j(x)P_k(x)$,如此一来,协变差函数以及转移概率就变成了如下的形式:
最后,结合克里金方法与转移概率,用转移概率矩阵表达上述普通克里金方程:
这样,通过转移概率利用克里金进行空间插值就得到了实现。
参考文献:
克里金(Kriging)插值的原理与公式推导:https://xg1990.com/blog/archives/222
董英, 基于随机水文地质结构的华北平原地下水流模拟研究, 2006, 中国地质大学(北京).