理想磁流体力学与霍尔磁流体力学下平行传播电磁波的色散关系推导

1.Derive the dispersion relation for low frequency plasma waves at parallel propagation in ideal MHD.

We assume $\mathbf{k} = k_\parallel \hat{z}$, and $\mathbf{B}_0 = B_0 \hat{z}$. Give the linearization of ideal MHD that:

$$\begin{equation} \begin{aligned} \omega \rho_1 &= \rho_0(\mathbf{k} \cdot \mathbf{u_1}), \\ \omega \rho_0 \mathbf{u_1} &= i \mathbf{J}_1 \times \mathbf{B_0} + p_1 \mathbf{k}, \\ \mu_0 \omega \mathbf{J_1} &= -i \mathbf{k} \times [\mathbf{k} \times (\mathbf{u_1} \times \mathbf{B_0})], \\ \omega \mathbf{B_1} &= - \mathbf{k} \times (\mathbf{u_1} \times \mathbf{B_0}), \\ \omega p_1 &= \gamma p_0 (\mathbf{k} \cdot \mathbf{u_1}). \end{aligned} \end{equation}$$

that we have:

$$\begin{equation} \begin{aligned} \mathbf{u_1} \times \mathbf{B_0} &= u_{1y} B_0 \hat{x} - u_{1x} B_0 \hat{y}, \\ \mathbf{k} \times (\mathbf{u}_{1} \times \mathbf{B}_{0})&= k_{\parallel} u_{1 x} B_{0} \hat{x}+k_{\|} u_{1 y} B_{0} \hat{y}, \\ \mathbf{k} \times [\mathbf{k} \times (\mathbf{u_1} \times \mathbf{B_0})] &= k_{\parallel}^2 u_{1x} B_0 \hat{y} - k_{\parallel}^2 u_{1y} B_0 \hat{x}. \end{aligned} \end{equation}$$

then we can obtain that:

$$\begin{equation} \begin{aligned} \mathbf{J_1} &= \frac{-i}{\mu_0 \omega} \mathbf{k} \times [\mathbf{k} \times (\mathbf{u_1} \times \mathbf{B_0})] \\ &= \frac{-i}{\mu_0 \omega} (k_{\parallel}^2 u_{1x} B_0 \hat{y} - k_{\parallel}^2 u_{1y} B_0 \hat{x}) \\ \Rightarrow i \mathbf{J_1} \times \mathbf{B_0} &= \frac{1}{\mu_0 \omega} ((k_{\parallel}^2 u_{1x} B_0^2 \hat{y} - k_{\parallel}^2 u_{1y} B_0^2 \hat{x})) \end{aligned} \end{equation}$$

and:

$$\begin{equation} \begin{aligned} p_1 &= \frac{\gamma p_0 ( \mathbf{k} \cdot \mathbf{u_1})}{\omega} \\ &= \frac{\gamma p_0 k_{\parallel} u_{1z}}{\omega} \end{aligned} \end{equation}$$

combine the formula (3) and (4), we can get:

$$\begin{equation} \begin{aligned} \omega \rho_0 \mathbf{u_1} &= i \mathbf{J}_1 \times \mathbf{B_0} + p_1 \mathbf{k} \\ &= \frac{-k_{\parallel}^2 u_{1y} B_0^2}{\mu_0 \omega} \hat{x} + \frac{k_{\parallel}^2 u_{1x} B_0^2}{\mu_0 \omega} \hat{y} + \frac{k_{\parallel}^2 \gamma p_0 u_{1z}}{\omega} \hat{z} \\ \end{aligned} \end{equation}$$ $$\begin{equation} \begin{aligned} \Rightarrow &\left\{\begin{array}{cc} \omega \rho_0 u_{1x} &= \frac{-k_{\parallel}^2 u_{1y} B_0^2}{\mu_0 \omega} \\ \omega \rho_0 u_{1y} &= \frac{k_{\parallel}^2 u_{1x} B_0^2}{\mu_0 \omega} \\ \omega \rho_0 u_{1z} &= \frac{k_{\parallel}^2 \gamma p_0 u_{1z}}{\omega} \end{array}\right. \end{aligned} \end{equation}$$

we can get tow solutions, one is from the z component that:

$$\begin{equation} \begin{aligned} \omega \rho_0 u_{1z} &= \frac{\gamma k_{\parallel}^2 p_0 u_{1z}}{\omega} \\ \Rightarrow \frac{\omega}{k_{\parallel}} &= \sqrt{\frac{\gamma p_0}{\rho_0}} = C_s \end{aligned} \end{equation}$$

and another one is:

$$\begin{equation} \begin{aligned} \omega \rho_0 u_{1x} &= \frac{-k_{\parallel}^2 u_{1y} B_0^2}{\mu_0 \omega} \\ \Rightarrow u_{1x} &= \frac{-k_{\parallel}^2 u_{1y} B_0^2}{\mu_0 \omega^2 \rho_0} \\ \Rightarrow \omega \rho_0 u_{1y} &= \frac{k_{\parallel}^2 u_{1x} B_0^2}{\mu_0 \omega} \\ &= \frac{-k_{\parallel}^4 u_{1y} B_0^4}{u_0^2 \omega^3 \rho_0} \\ \Rightarrow \frac{\omega}{k_{\parallel}} &= \sqrt{\frac{B_0^2}{\mu_0 \rho_0}} = V_{A} \end{aligned} \end{equation}$$

2.Redo the above analysis by keeping the Hall term in the generalized Ohm’s law.

Like the procedure of Ideal-MHD, from the Maxwell equations we can obtain that:

$$\begin{equation} \begin{aligned} \mathbf{k} \times (\mathbf{k} \times \mathbf{E_1}) = -i \omega \mu_0 \mathbf{J_1} \end{aligned} \end{equation}$$

and Generalized Ohm’s law:

$$\begin{equation} \begin{aligned} \mathbf{E_1} = \frac{1}{n_0 e} \mathbf{J_1} \times \mathbf{B_0}-\mathbf{u_1} \times \mathbf{B_0} \end{aligned} \end{equation}$$

so that:

$$\begin{equation} \begin{aligned} \mathbf{k} \times (\mathbf{k} \times (\frac{1}{n_0 e} \mathbf{J_1} \times \mathbf{B_0}-\mathbf{u_1} \times \mathbf{B_0})) = -i \omega \mu_0 \mathbf{J_1} \end{aligned} \end{equation}$$

with:

$$\begin{equation} \begin{aligned} &\mathbf{k} = k_{\parallel} \hat{z} \\ &\mathbf{B_0} = B_0 \hat{z} \\ &\mathbf{u_1} = u_{1x} \hat{x} + u_{1y} \hat{y} + u_{1z} \hat{z} \\ \end{aligned} \end{equation}$$

to get the $\mathbf{J_1}$:

$$\begin{equation} \begin{aligned} \mathbf{J_1} &= -\frac{e n_0 (B_0^2 k_{\parallel}^4 u_{1 x}-i B_0 e k_{\parallel}^2 \mu_0 n_0 \omega u_{1 y})}{- B_0^2 k_{\parallel}^4 + e^2 \mu_0^2 n_0^2 \omega^2} \hat{x} \\ &+\frac{B_0 k_{\parallel}^2 (i e^2 \mu_0 n_0^2 \omega u_{1x} + B_0 e k_{\parallel}^2 n_0 u_{1y})}{B_0^2 k_{\parallel}^4 - e^2 \mu_0^2 n_0^2 \omega^2} \hat{y} \end{aligned} \end{equation}$$

put it into the momentum equation that: $\omega \rho_0 \mathbf{u_1} = i \mathbf{J}_1 \times \mathbf{B_0} + p_1 \mathbf{k}$, we have:

$$\begin{equation} \begin{aligned} \left \{ \begin{array}{cl} -i \omega \rho_0 u_{1x} &= \frac{B_0^2 k_{\parallel}^2 (i e^2 \mu_0 n_0^2 \omega u_{1x} + B_0 e k_{\parallel}^2 n_0 u_{1y})}{B_0^2 k_{\parallel}^4 - e^2 \mu_0^2 n_0^2 \omega^2} \\ -i \omega \rho_0 u_{1y} &= \frac{B_0^2 e k_{\parallel}^2 n_0 (-B_0 k_{\parallel}^2 u_{1x} + i e \mu_0 n_0 \omega u_{1y})}{B_0^2 k_{\parallel}^4 - e^2 \mu_0^2 n_0^2 \omega^2} \\ -i \omega \rho_0 u_{1z} &= - \frac{i k_{\parallel}^2 p_0 u_{1z} \gamma}{\omega} \end{array} \right. \end{aligned} \end{equation}$$

with the $\rho_0 = n_0 (m_i+m_e) \approx n_0 m_i$ and $p_0 = n_0 k_B T$, the z component demonstrate that:

$$\begin{equation} \begin{aligned} \omega^2 = k_{\parallel} \frac{\gamma k_B T}{m_i} \end{aligned} \end{equation}$$

rewrite the x, y component into the form of below:

$$\begin{equation} \begin{aligned}\left \{\begin{array}{cl} u_{1x} -\frac{i B_0^3 e k_{\parallel}^4 n_0}{\omega (-B_0^2 e^2 k_{\parallel}^2 \mu_0 n_0^2 - B_0^2 k_{\parallel}^4 \rho_0 + e^2 \mu_0^2 n_0^2 \omega^2 \rho_0)} u_{1y} &= 0\\ \frac{i B_0^3 e k_{\parallel}^4 n_0}{\omega (-B_0^2 e^2 k_{\parallel}^2 \mu_0 n_0^2 - B_0^2 k_{\parallel}^4 \rho_0 + e^2 \mu_0^2 n_0^2 \omega^2 \rho_0)} u_{1x} - u_{1y} &= 0 \end{array}\right.\end{aligned} \end{equation}$$

to have a solution, the coefficient determinant must be zero, it means that:

$$\begin{equation} \begin{aligned} &\frac{B_0^6 e^2 k_{\parallel}^8 n_0^2}{(-B_0^2 k_{\parallel}^2 (k{\parallel}^2 m_i n_0 + e^2 n_0^2 \mu_0) \omega + e^2 m_i n_0^3 \mu_0^2 \omega^3)^2} = 1 \\ \Rightarrow &\pm B_0^3 e k_{\parallel}^4 n_0 - B_0^2 k_{\parallel}^2 (k{\parallel}^2 m_i n_0 + e^2 n_0^2 \mu_0) \omega + e^2 m_i n_0^3 \mu_0^2 \omega^3 = 0 \\ \Rightarrow &\frac{m_i^2 e^2 m_i n_0^3 \mu_0^2 \omega^3}{e^5 B_0^3 \mu_0^2 n_0^3} - \frac{m_i^2 B_0^2 k_{\parallel}^2 \omega}{e^5 B_0^3 \mu_0^2 n_0^3} (k{\parallel}^2 m_i n_0 + e^2 n_0^2 \mu_0) \pm \frac{m_i^2 B_0^3 e k_{\parallel}^4 n_0}{e^5 B_0^3 \mu_0^2 n_0^3} = 0 \\ \Rightarrow &\frac{m_i^3 \omega^3}{e^3 B_0^3} - \frac{m_i^2 k_{\parallel}^2 \omega}{e^5 B_0 \mu_0^2 n_0^3} (k{\parallel}^2 m_i n_0 + e^2 n_0^2 \mu_0) \pm \frac{m_i^2 k_{\parallel}^4}{e^4 \mu_0^2 n_0^2} = 0 \end{aligned} \end{equation}$$

with the $\Omega_i = \frac{e B_0}{m_i}$, $\lambda_i = \sqrt{\frac{m_i}{\mu_0 n_0 e^2}}$, we can derive that:

$$\begin{equation} \begin{aligned} (\frac{\omega}{\Omega_i})^3 - k_{\parallel}^2 \lambda_i^2 (1 + k_{\parallel}^2 \lambda_i^2)(\frac{\omega}{\Omega_i}) \pm k_{\parallel}^4 \lambda_i^4 = 0 \end{aligned} \end{equation}$$

it can be reduced to a simpler form by consider the factorization of the trem that can’t be zero.

$$\begin{equation} \begin{aligned} k^2\lambda^2 \frac{\omega}{\Omega}-k^2 \lambda^2 + \frac{\omega^2}{\Omega^2} = 0 \end{aligned} \end{equation}$$

3.Solve the dispersion relation s obtained in Problem 2 numerically. Plot the dispersion relations and discuss the difference between the ideal and Hall MHD dispersion relations.

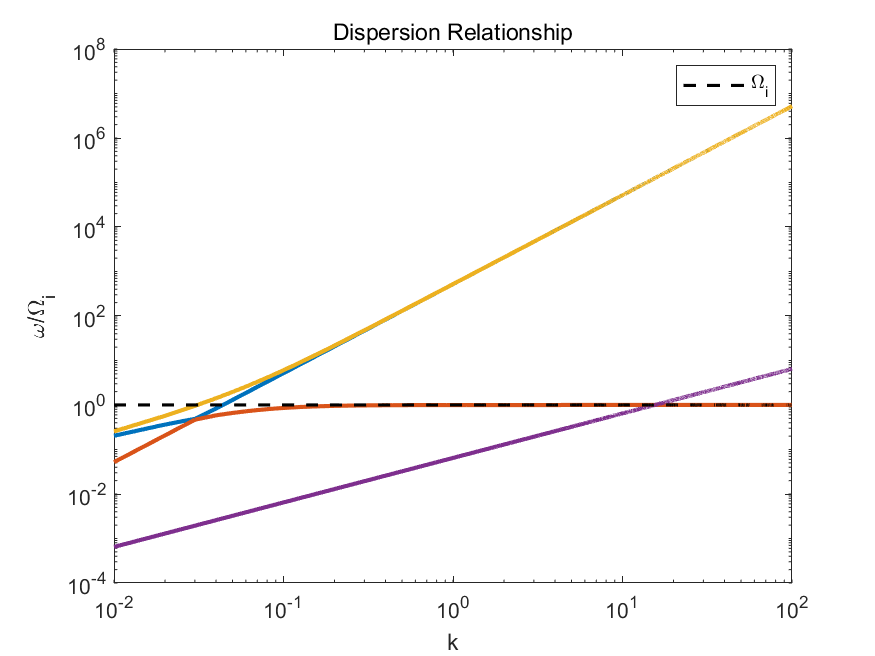
the figure of the dispersion is:

the difference between the ideal MHD and Hall MHD dispersion relations is the x, y component contribute a Fast Magnetic wave which is coincident with the Alfven wave at the low frequency but the Ideal MHD has only the Alfven wave term. It has three positive solution roots for the dispersion equations that we can draw three curve to illustrate it. Besides this, we can also find a resonant phenomenon when the $\mathbf{k}$ is sufficient large. The Red dotted line is the false root because of the general division operation in solving process.

the code to plot the dispersion has been presented below:

clear;
clc;
n0=1*10^8;
mi=1.67*10^(-27);
e = 1.6*10^(-16); B = 5*10^4*10^-9; Epsilon0 = 8.85*10^(-12); c = 3*10^8;mu0=4*pi*10^(-7);
gamma = 1;kBT = 1*e;
% wpei2 = (ni*e^2)./(Epsilon0*mi);
Omegai = (e*B)/mi;
lambdai = sqrt(mi/(e^2*mu0*n0));
% kk=0:1e-2:100;
kk = linspace(0,100,10000);
w=[];
w2=[];
w3=[];
line=[];
for k=kk
    p=[1/Omegai^3,0,-(k^2*lambdai^2*(1+k^2*lambdai^2))/Omegai,k^4*lambdai^4];
    p2=[1/Omegai^3,0,-(k^2*lambdai^2*(1+k^2*lambdai^2))/Omegai,-k^4*lambdai^4];
    p3=[1,0,-k^2*(gamma*kBT)/mi];
    omg=roots(p); w=[w,omg];
    omg2=roots(p2); w2=[w2,omg2];
    omg3=roots(p3); w3=[w3,omg3];
    line=[line,1];
end
w11=w(1,:)./Omegai;
w12=w(2,:)./Omegai;
w13=w(3,:)./Omegai;
w21=w2(1,:)./Omegai;
w22=w2(2,:)./Omegai;
w23=w2(3,:)./Omegai;
w31=w3(1,:)./Omegai;
w32=w3(2,:)./Omegai;

%%

figure(1);
clf;
% set(gca,'LineWidth',2);
% w11, w22, w23, w32 为负根，舍弃
loglog(kk,w12,kk,w13,kk,w21,kk,w31,'LineWidth',2);
hold on;
% legend('11','12','13','21','22','23','31','32');
p1=loglog(kk,line,'k--','LineWidth',1.5);
legend(p1,'\Omega_i')
xlabel('k');
ylabel('\omega/\Omega_{i}');
title('Dispersion Relationship');

saveas(gca, '3.png');