第一部分拉格朗日力学原理

Highlight：

最小作用量原理是怎么来的;
拉格朗日函数是怎么来的;
最小作用量原理、拉格朗日函数、牛顿经典力学原理之间的自洽;

最小作用量原理

物理学关注的本质是世间万物的运动, 即系统状态随时空的演化, 抽象到数学就是微分方程系统的演化.

在牛顿的世界观里, 意思是力是改变物体运动的原因, 存在力和加速度之间的表达式 $\vec{F} = m a$ . 在这样的观点下, 考察物体的状态就必须要对物体进行受力分析, 但很多时候(比如存在约束的时候)我们没有办法完全确定物体所受的力(因为约束限制的是物体的运动, 它对物体作用的力会随着物体运动的不同而发生改变, 和物体的运动一样是一个待确定的量), 因此牛顿力学的诸多限制促使我们寻求另外一种对物体运动的思考方式, 这种思考方式更加接近于事物的本质, 如果说牛顿运动定律是牛顿通过自然观察总结出来的定律, 那么接下来我们讨论的就可能是万物运动所遵循的最基本的法则, 自然机器的”底层逻辑”——最小作用量原理.

所谓最小作用量原理其实是一个很符合哲学概念的假设, 即万事万物的运动总是以牺牲最小的代价为原则, 这个代价在物理学上就被定义为作用量, 实际上这个概念来自自然界中各种极值现象, 比如光总是走最短的路线, 或者液滴总是呈现表面积最大的球形. 当然也可能人的经验感觉在这个概念的发展过程中起到了重要的作用, 比如让球从曲面的高处落下时通常会沿着梯度最大的方向运动, 总的来说追求极值的状态是一件自然而然的事情. 一旦我们接受了这样的原理(事实上我们也很容易就能接受这样的假设), 就会发现它似乎可以解释我们所面临的所有相关问题.

从能量谈起

关于物体的运动或者说物体的状态, “能量” 是一个绝对绕不开的名词, 人们从日常生活中提炼的第一个深刻思想便是能量守恒, 最早追溯到莱布尼兹, 他指出: 以落体运动来说，物体升起的高度是与初速度的平方成正比，因之作用在物体上的力的效应必定是与其重量所给予的速度平方而不是速度成正比的，这就是机械能守恒的最早的形式, 即重力势能和动能的相互转化. 物理学的发展过程中提出过很多种能量的概念, 但最终回到粒子层面就只存在两种能量的形式:

动能
势能

实际上这就是构成机械能守恒的两种能量形式, 同时在牛顿力学的基础上, 我们有:

\begin{matrix} (1) & \begin{array}{r} F (x) = - \frac{d V (x)}{d x} \end{array} \end{matrix}

也就是说势能函数的定义可以通过上式的积分操作给出:

\begin{matrix} (2) & \begin{array}{r} V (x) = - \int F (x) d x \end{array} \end{matrix}

对于上面这个式子的表述换句话说就是力总是沿着具有更低势能的方向来推动粒子, 同时势能函数越陡峭, 力就越大. 并且, 根据势能和动能之和守恒, 沿着势能函数降低时动能( $1 / 2 m v^{2}$ )将增加, 势能函数的时间导数( $v d V / d x$ )对应了动能的时间导数( $m v \dot{v}$ ), 所以很自然的势能越陡峭, 力就越大, 同时粒子的加速度越大, 这样就得到牛顿运动定律的表述形式.

这里有一个很重要的问题, 即存在力决定势能还是存在势能决定力? 牛顿力学体系中力是一个实实在在的概念, 因为通常我们面对的是相互接触的物体, 但如果对象变成苹果和地球, 或者粒子与粒子时力的概念就变得抽象起来. 另外对于物质弱耦合态(比如无碰撞等离子体)的压强的讨论也是一个很值得思考的问题, 通过统计力学(动理论)的方式推导出来动量方程中的压强梯度项实际上就是来自于动量本身的变化, 其作用形式和力的概念相似, 所以我们定义其为压强梯度力. 因此我们也许可以说实际上决定物体如何运动的是能量的变化, 运动即势能和动能相互转化的过程, 这个过程是通过力的概念来完成和体现的.

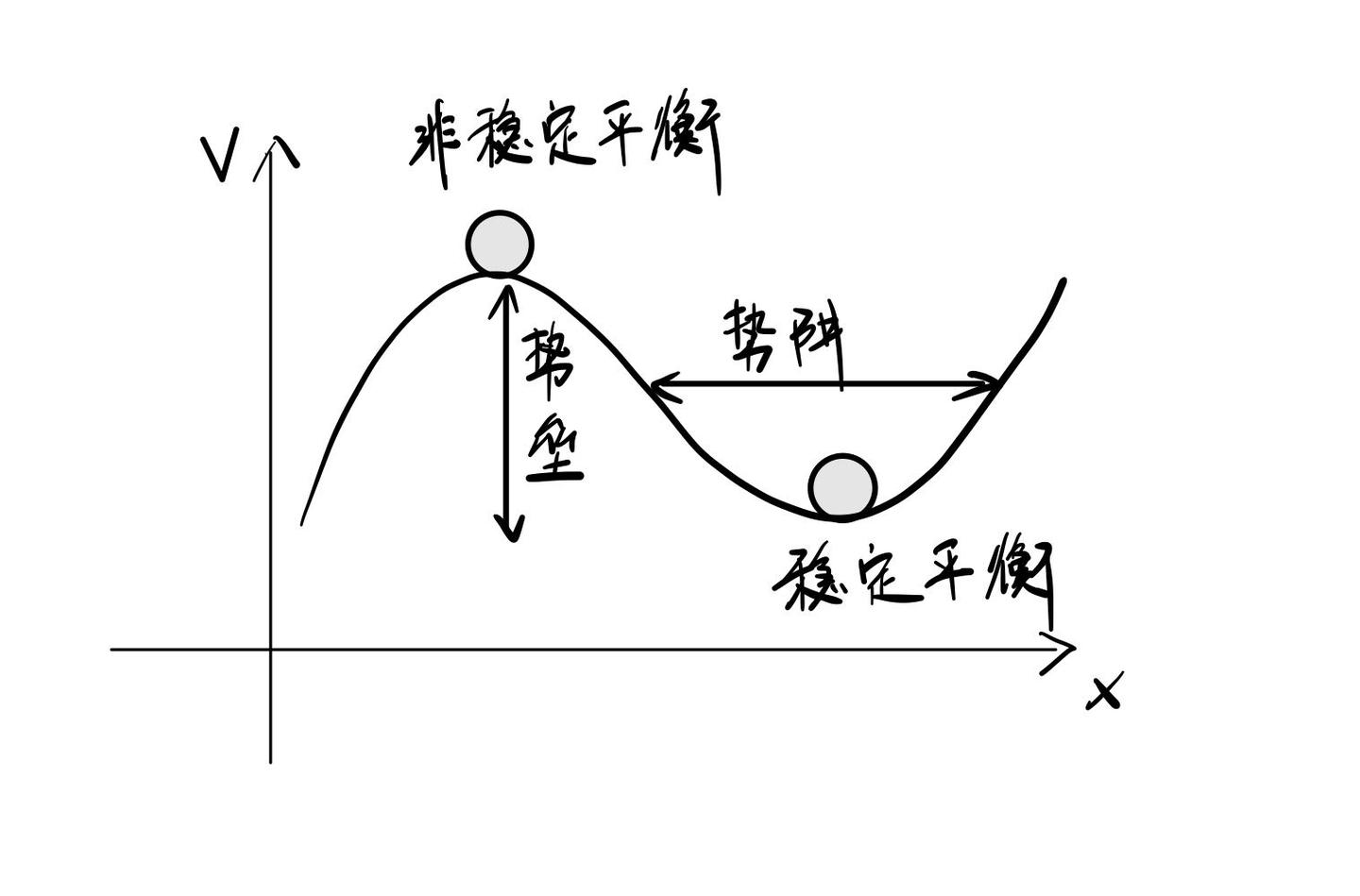
在能量的概念下讨论物体的状态时, 我们经常能够听到稳态或者平衡的说法, 根据牛顿力学, 力是改变物体运动状态的原因, 而力是势能函数的梯度, 这样一来势能函数的形状就决定了物体保持原本状态的能力, 即平衡的能力. 从数学上来说, 如果系统势能位于势能函数的极值处, 即:

\begin{matrix} (3) & \begin{array}{r} \frac{d V}{d x} = 0 \end{array} \end{matrix}

时称作平衡态, 按照极大值点和极小值点又可以分为”非稳定平衡态”和”稳定平衡态”. 同时一个系统可能具有多个平衡态(势能函数具有多个极值点), 平衡态之间的位置称为”势阱”和”势垒”.

经验告诉我们, 物体总是趋向于处于能量更低的状态, 换句话说就是, 如果暂时不考虑物体从一个状态变化到另一个状态的中间过程(运动过程), 物体下一个时刻的状态可以完全自由选择的话, 物体总是会倾向于选择能量最低的那一种状态, 对人来说就相当于是选择最轻松的状态. 这么说来, 宇宙也喜欢躺平(躺平是在遵循自然地法则O(∩_∩)O哈哈~).

对作用量的思考

上面的这种原则给出了在多个状态之间的选择, 那么对于目前的状态和被选择的能量最低的状态之间的过程, 即: 物体如何选择从一个状态到另一个状态之间的运动呢?

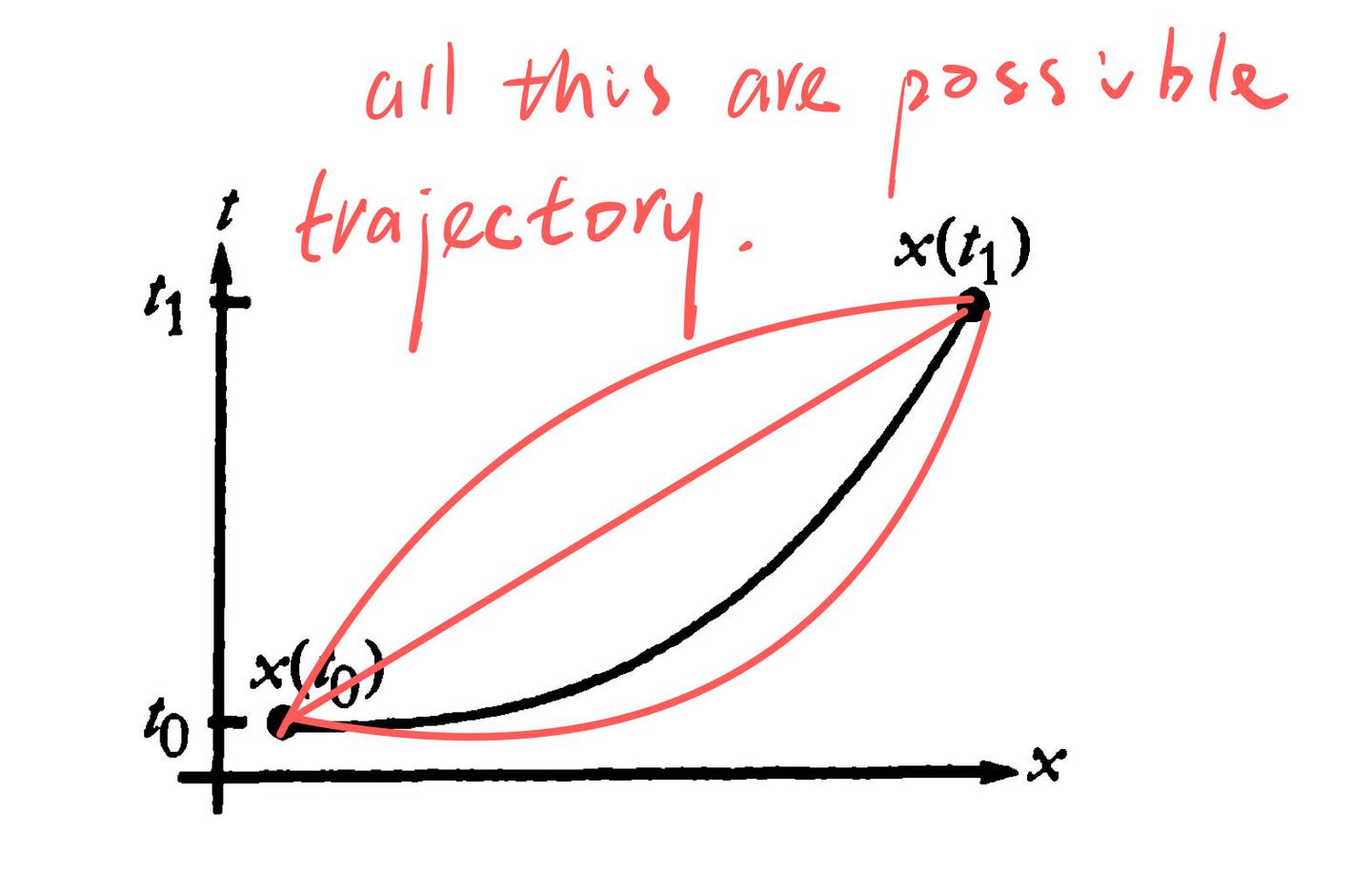
换成一个最简单的力学问题, 上面的这个问题被表述为: 如果我们知道初始时刻 $t_{0}$ 和运动之后某一时刻 $t_{1}$ 的位置 $x_{0}$ , $x_{1}$ , 在不知道其他条件的情况下有办法确定出物体在这个时间段内的运动吗? 从牛顿力学的观点来看这几乎是一个不可能的问题, 牛顿力学需要知道初始状态( $x_{0}$ )以及受力( $F$ , 实际上是 $\ddot{x}$ )然后对未来甚至是过去进行预测或者回溯, 相当于在 $x - t$ 坐标下知道曲线上的一个点和曲线(上每一个点)的方向, 也就是已经知道该怎么画出这条曲线了. 而现在的问题是确定一条连接已知两个点的曲线, 我们可以有无数种选择方式, 但大自然最终只会有一条确定的曲线, 我们想知道的就是造物主是如何确定这条曲线的!

对比之前不同状态之间的选择, 加上各种自然现象给我们的暗示, 我们可以很自然的做出那个从哲学上来说是如此的优美的假设. 既然我们的造物主这么喜欢极值, 说不定对于路径的选择也是遵循某种极值法则来的. 也就是说, 每一种运动方式, 即每一条路径都对应了一个数(这个数被我们称作 “作用量”), 在上面的图中, 很显然这个数是 $x (t_{0})$ 和 $x (t_{1})$ 之间的运动的积分. 这个不同运动对应的数, 或者说运动对应的函数我们用 $L$ 来表示, 描述空间中的运动需要两个量: 位置 $q$ 和速度 $\dot{q}$ , 再加上单独的时间维, 我们可以确定出一个描述力学体系运动的函数:

\begin{matrix} (4) & \begin{array}{r} L (q_{i}, {\dot{q}}_{i}, t) \end{array} \end{matrix}

那么作用量就被表述为:

\begin{matrix} (5) & \begin{array}{r} A = \int_{t_{0}}^{t_{1}} L (q_{i}, {\dot{q}}_{i}, t) d t \end{array} \end{matrix}

也就是说作用量 $A$ 实际上是函数 $L$ 的积分, 通过变分法求出满足使得 $A$ 得极小值的函数 $L$ 即可, 其对应的运动形式就是自然在无数条轨迹中选择的那一条.

拉格朗日函数

上面的内容中我们假设了世界遵循的一般规律, 即最小作用量原理, 这一部分我们就直接尝试从最小作用量原理推出物体运动的方程, 来看看世界选择的运动形式是什么样的.

首先应该注意到, 我们的作用量作为函数是不依赖于时间的, 这与描述运动的 $L$ 函数不同, $L$ 通过 $q (t)$ , $\dot{q} (t)$ 隐含了最终变量 $t$ , 但是在 $L$ 到作用量 $A$ 的积分中, $t$ 已经被积分掉了, 因此作用量依赖的不再是时间 $t$ 而是 $q (t)$ 的函数形式, 是函数到数的映射. 对这样一个依赖于函数的函数作微分的操作来自于数学的泛函分析, 即”变分法”, 其过程和处理数到数的映射的微积分类似.

现在我们要求对作用量 $A$ 的变分 $δ A = 0$ , 作为作用量取到极值的条件. 即我们需要挑选出满足下面两个条件的函数 $q (t)$ :

\begin{matrix} (6) & \begin{array}{r} {\begin{cases} q (t_{0}) = q_{0}, q (t_{1}) = q_{1} \\ δ A = δ \int_{t_{0}}^{t_{1}} L (q (t), \dot{q} (t), t) d t = 0 \end{cases} \end{array} \end{matrix}

重点是第二项的变分, 我们将其单独拿出来分析:

\begin{matrix} (7) & \begin{aligned} δ A & = δ \int_{t_{0}}^{t_{1}} L (q (t), \dot{q} (t), t) d t \\ = \int_{t_{0}}^{t_{1}} \sum_{i} (\frac{\partial L}{\partial q_{i}} δ q_{i} + \frac{\partial L}{\partial {\dot{q}}_{i}} δ {\dot{q}}_{i}) d t \end{aligned} \end{matrix}

其中, $δ {\dot{q}}_{i}$ 变分和微分可以交换次序, 即 $δ {\dot{q}}_{i} = d / d t (δ q_{i})$ , 那么上式的被积分的第二项可以变为:

\begin{matrix} (8) & \begin{aligned} \int_{t_{0}}^{t_{1}} \sum_{i} \frac{\partial L}{\partial {\dot{q}}_{i}} \frac{d}{d t} (δ q_{i}) d t \\ = \int_{t_{0}}^{t_{1}} \frac{\partial L}{\partial {\dot{q}}_{i}} d (δ q_{i}) \\ = {\sum_{i} \frac{\partial L}{\partial {\dot{q}}_{i}} δ q_{i} |}_{t_{0}}^{t_{1}} - \int_{t_{0}}^{t_{1}} \sum_{i} δ q_{i} d (\frac{\partial L}{\partial {\dot{q}}_{i}}) \end{aligned} \end{matrix}

其中由于 $t_{1}$ 和 $t_{2}$ 时刻的位置都是固定的, 所以 $δ q_{i}$ 在这两个位置都为零, 即上式第一项为零, 第二项有:

\begin{matrix} (9) & \begin{array}{r} δ q_{i} d (\frac{\partial L}{\partial {\dot{q}}_{i}}) = δ q_{i} \frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{i}}) d t \end{array} \end{matrix}

将上述结论代回到 $(6)$ 式中, 有:

\begin{matrix} (10) & \begin{array}{r} δ A = \int_{t_{0}}^{t_{1}} \sum_{i} (\frac{\partial L}{\partial q_{i}} - \frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{i}}) δ q_{i}) d t = 0 \end{array} \end{matrix}

要求 $L$ 满足上式, 只能是:

\begin{matrix} (11) & \begin{array}{r} \frac{\partial L}{\partial q_{i}} - \frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{i}}) = 0 \end{array} \end{matrix}

对所有的 $i$ 都成立才行. 这就是拉格朗日方程, 它就是自然界选择的实际运动所满足的微分方程, 其中对运动进行描述的量 $L$ 被称为 拉格朗日量 或者 拉格朗日函数. 可以指出的是, 一个拉格朗日函数对应了一个力学体系, 但一个力学体系却可以有多个拉格朗日函数来表述, 这是由于两个不同的拉格朗日函数各自得到的作用量的变分可能是一样的. 实际上表述出来为:

$L = L (q, \dot{q}, t)$ 与 $L^{'} = L (q, \dot{q}, t) + \frac{d}{d t} f (q, t)$ 描述的是同一个力学系统.

从拉格朗日力学到牛顿力学

上面的过程虽然给出了一个运动对应的拉格朗日函数以及它所需要满足的微分方程, 但这个函数的具体形式还尚不清楚, 对于具体的问题我们也没法直接上手分析, 所以这一部分的内容就来讨论这个函数的具体形式是什么样的, 实际上就是将拉格朗日力学与牛顿力学建立起联系的过程.

参考系的选择对于一个力学体系的研究来说是非常重要的, 按照现代引力理论的观点, 引力并不是实际存在的力, 而时空的不均匀性引起的物体运动状态的改变, 即在现实的任意的参考系(地球)中, 时空的不均匀性将会导致不受外力作用的物体无法保持静止. 但是我们总能找到一个参考系, 时空间相对它来说是均匀且各向同性的, 这样的参考系称为: 惯性参考系, 在这样的参考系中, 自由(没有外力作用的情况下)物体将会永远保持它的运动状态.

对于这样一个惯性系中自由运动的质点, 时间和空间的均匀性意味着运动对应的函数不显含时间 $t$ 和位置 $q$ , 这样一来, $L$ 就只能是速度 $v$ 的函数. 同时, 空间的各向同性意味着速度的方向不会影响运动, 拉格朗日量应该只取决于速度的大小, 对于速度这样一个矢量来说, 平方之后的量刚好能够满足条件, 即:

\begin{matrix} (12) & \begin{array}{r} L = L (v^{2}) = L (v^{2}) \end{array} \end{matrix}

同时, 由于拉格朗日函数不显含位置矢量, 即 $\partial L / \partial r = 0$ , 其满足的拉格朗日方程就变成:

\begin{matrix} (13) & \begin{aligned} \frac{d}{d t} \frac{\partial L}{\partial \dot{r}} = 0 \\ ⟹ \frac{\partial L}{\partial v} = const \end{aligned} \end{matrix}

根据公式 $(12)$ :

\begin{matrix} (14) & \begin{aligned} \frac{\partial L (v^{2})}{\partial v} = \frac{\partial L}{\partial v} \cdot 2 v = const \\ ⟹ const \cdot 2 v = const \\ ⟹ v = const \end{aligned} \end{matrix}

这样我们从时空间均匀且各向同性的假设出发, 推出来了这样的参考系中自由物体运动状态不变的惯性定理.

如果此时我们引入另外一个惯性参考系, 它相对于第一个惯性系作匀速直线运动, 根据时空间均匀且各向同性的性质, 自由物体在这两个不同的惯性参考系中的运动应该是等价的, 力学规律是相同的, 这就是伽利略相对性原理. 那么我们假设现在有两个惯性系 $K$ 和 $K^{'}$ , 两者之间以一个无穷小的速度 $ϵ$ 相对运动, 根据拉格朗日量和速度的平方有关, 我们可以得到:

\begin{matrix} (15) & \begin{array}{r} L^{'} = L (v^{' 2}) = L (v^{2} + 2 v \cdot ϵ + ϵ^{2}) \end{array} \end{matrix}

将这个式子对无穷小量 $ϵ$ 进行泰勒展开, 忽略高阶无穷小项:

\begin{matrix} (16) & \begin{array}{r} L (v^{' 2}) = L (v^{2}) + 2 \frac{\partial L}{\partial v^{2}} v \cdot ϵ \end{array} \end{matrix}

由于 $K$ 和 $K^{'}$ 都是惯性系, 所以应该满足关系:

L (v^{' 2}) = L (v^{2}) + \frac{d}{d t} f (r, t) = L (v^{2}) + \frac{\partial f}{\partial r} \cdot v + \frac{\partial f}{\partial t}

即式 $(16)$ 中的第二项要作为时间的全导数存在, 而且惯性系中的拉格朗日量不显含时间, 那么我们有:

\begin{matrix} (17) & \begin{array}{r} 2 \frac{\partial L}{\partial v^{2}} ϵ = \frac{\partial f}{\partial r} \end{array} \end{matrix}

这个式子左边不含有 $r$ , 右边不含有 $v$ , 还要求左右相等, 只能是两边都等于一个常数, 令这个常数为: $m ϵ$ , 则可以得到自由质点的拉格朗日量为:

\begin{matrix} (18) & \begin{array}{r} L = \frac{1}{2} m v^{2} \end{array} \end{matrix}

其中, $m$ 被定义为质量.

这样可以得到无相互作用的质点系的拉格朗日量为:

\begin{matrix} (19) & \begin{array}{r} L = \sum_{α} \frac{m_{α} v_{α}^{2}}{2} \end{array} \end{matrix}

对于存在相互作用的自由质点系(质点系内存在相互作用, 但整个质点系不受到任何外力作用), 需要考虑相互作用对拉格朗日量的影响, 这一项必然包含多个质点的坐标, 即:

\begin{matrix} (20) & \begin{array}{r} L = \sum_{α} \frac{1}{2} m_{α} v_{α}^{2} + G (r_{1}, r_{2}, r_{3}, \dots, r_{N}, t) \end{array} \end{matrix}

其中, 我们将第一部分无相互作用质点系的拉格朗日函数表示为 $T$ , 根据之前牛顿力学的结论我们知道这实际上就是质点系的动能, 后续我们将给出它的一般含义. 而后面相互作用对拉格朗日量的影响我们设定为只和所有质点在同一时刻的位置有关, 并且这种相互作用时瞬时传递的, 只有这样才能满足伽利略相对性原理, 这在朗道的书中有更详细的描述, 同时由于时间的各向同性, 证明我们的力学系统是可逆的, 这一点是所有经典力学成立的前提.

通过上面的拉格朗日函数的形式, 结合运动满足的拉格朗日方程, 有:

\begin{matrix} (21) & \begin{aligned} \frac{\partial L}{\partial r_{α}} & = \frac{d}{d t} \frac{\partial L}{\partial v_{α}} \\ ⟹ \frac{\partial G}{\partial r_{α}} & = m_{α} a_{α} = F_{α} \end{aligned} \end{matrix}

对上述过程如果令 $G = - V$ , 那就直接回到了之前牛顿力学的形式, 即:

F = - \frac{\partial V}{\partial r}

其中, $V$ 就是势能函数, 表示质点系中的相互作用. 同时拉格朗日函数形式变成了:

\begin{matrix} (22) & \begin{array}{r} L = T - V \end{array} \end{matrix}

这就是我们常见的拉格朗日函数形式了.